Johannes Kepler
De coni sectionibus / Über die Kegelschnitte
Latin and German
Edited and translated by Thomas Dittert
Neujahrsgabe 1990
Ad Vitellionem paralipomena quibus Astronomiae Pars Optica traditur
Frankfurt 1604
Chapter IV, Section 4 (Latin - German)
Messekunst Archimedis
Linz 1616
Erster Thail, No. 29-31 (original German)
KEPLER'S Ad Vitellionem paralipomena of 1604, a milestone in the history of geometrical optics, contain an original discourse on conic sections. KEPLER refers to Apollonius and to the commentary of Eutocius, but his study is quite distinct from the treatment of conic sections found in the works of his predecessors. He was the first mathematician to discuss the hyperbola, the parabola, the ellipse, and the circle as curves transforming continuously from one into another, in such a manner »that the straight line transforms through an infinity of hyperbolas into the parabola and then through infinitely many ellipses into the circle«.
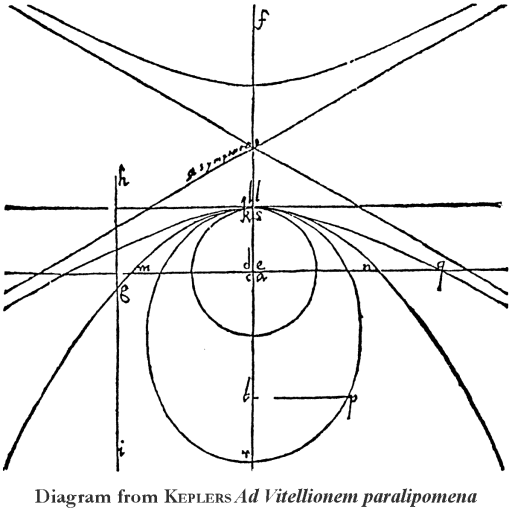So when KEPLER points out the significance of the focus (here we find the first appearance of this term in western mathematics!) he interprets the parabola as a hyperbola or an ellipse with an infinitely distant focus that occurs at both ends of the axis and is the meeting point of all lines running parallel to the axis. Afterwards, he explains the string constructions for the hyperbola and the ellipse, followed by the corresponding construction for the parabola which he had invented by this same analogy.
KEPLER appreciates the role of analogy as a means of discovery:
»Oportet enim nobis servire voces Geometricas analogiae: Plurimum namque amo analogias, fidelissimos meos magistros, omnium naturae arcanorum conscios: in Geometria praecipue suspiciendos, dum infinitos casus interiectos intra sua extrema, mediumque, quantumvis absurdis locutionibus concludunt, totamque rei alicuius essentiam luculenter ponunt ob oculos.«
»It is useful for us to have the geometric terms directed by analogy. For I love analogies above all: they are my most reliable masters, acquainted with all the secrets of nature. In geometry, one should hold them in high regard especially when they link together an infinite number of cases lying between the extremes and the mean - however discordant their language may be - and clearly present to our eyes the whole essence of any matter.«
The related section of Kepler's Messekunst Archimedis of 1616, written in his vigorous vernacular German, treats the same subject from a more popular point of view.
