Johannes Kepler
De coni sectionibus / Über die Kegelschnitte
Lateinisch und deutsch
Herausgegeben und übersetzt von Thomas Dittert
Neujahrsgabe 1990
Ad Vitellionem paralipomena quibus Astronomiae Pars Optica traditur
Frankfurt 1604
Kapitel IV, Abschnitt 4 (lateinisch - deutsch)
Messekunst Archimedis
Linz 1616
Erster Thail, No. 29-31 (Originalfassung)
In KEPLERS Ad Vitellionem paralipomena von 1604, einem Markstein in der Geschichte der geometrischen Optik, findet sich eine originelle Abhandlung über die Kegelschnitte. KEPLER nimmt Bezug auf Apollonius und den Kommentar von Eutocius, doch seine Untersuchung unterscheidet sich grundlegend von der Behandlung der Kegelschnitte in den Werken seiner Vorgänger. Er war der erste Mathematiker, der Hyperbel, Parabel, Ellipse und Kreis als kontinuierlich ineinander übergehende Kurven beschrieb, dergestalt, »dass die Gerade über eine unendliche Zahl von Hyperbeln in die Parabel und diese über unendlich viele Ellipsen in den Kreis übergeht«.
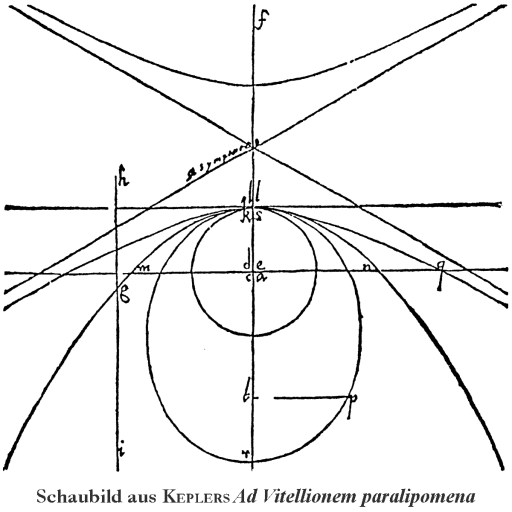Als KEPLER die Bedeutung des Brennpunkts zeigt (dieser Ausdruck taucht in der abendländischen Mathematik hier zum ersten Mal auf!), deutet er daher die Parabel als eine Hyperbel oder Ellipse mit einem unendlich fernen Brennpunkt, der sich an beiden Enden der Achse findet und Treffpunkt aller Achsenparallelen ist. Anschließend erklärt er die Fadenkonstruktionen für die Hyperbel und die Ellipse, gefolgt von der entsprechenden Konstruktion für die Parabel, die er über ebendiese Analogie gefunden hat.
KEPLER weiß die Hilfe der Analogie beim Entdecken zu würdigen:
»Oportet enim nobis servire voces Geometricas analogiae: Plurimum namque amo analogias, fidelissimos meos magistros, omnium naturae arcanorum conscios: in Geometria praecipue suspiciendos, dum infinitos casus interiectos intra sua extrema, mediumque, quantumvis absurdis locutionibus concludunt, totamque rei alicuius essentiam luculenter ponunt ob oculos.«
»Es ist zweckmäßig für uns, wenn sich die geometrischen Bezeichnungen nach der Analogie richten: die Analogien liebe ich nämlich über alles als meine zuverlässigsten Lehrmeister, die in alle Geheimnisse der Natur eingeweiht sind. In der Geometrie muß man vor allem dann große Achtung vor ihnen haben, wenn sie unzählige zwischen den Extremen und der Mitte liegende Fälle - und sei es auch in noch so befremdlicher Ausdrucksweise - zusammenschließen und das ganze Wesen einer Sache deutlich vor Augen führen.«
Der entsprechende Abschnitt aus KEPLERS Messekunst Archimedis von 1616, abgefaßt in seiner kernigen deutschen Mundart, behandelt dasselbe Thema in mehr populärer Betrachtungsweise.
